Temporal Properties

Intro

Invariants aren’t really part of TLA+. There’s no concept of an “invariant” that’s treated as special by TLA+. The model checker, TLC, gives us that, but more that’s due to pragmatics and efficiency than “invariants” being something deeply important. Rather, TLA+ provides a general principled way to write all kinds of different properties, where invariants are just one of many things we can check. To write these, we use a set of temporal operators to describe logical statements across time. We call the broad class of all properties temporal properties.

There are two kinds of temporal properties: “safety” properties say our system doesn’t do bad things. “liveness” properties say our system always does a good thing. “We do not violate any database constraints” is safety, “All transactions either complete or roll back” is a liveness property. All invariants are safety properties, but not all safety properties are invariants. For example:

---- MODULE orchestrator ----
EXTENDS Integers, TLC, FiniteSets

Servers == {"s1", "s2"}

(*--algorithm threads
variables 
  online = Servers;

process orchestrator = "orchestrator"
begin
  Change:
    while TRUE do
      with s \in Servers do
       either
          await s \notin online;
          online := online \union {s};
        or
          await s \in online;
          await Cardinality(online) > 1;
          online := online \ {s};
        end either;
      end with;
    end while;
end process;

end algorithm; *)
====

5 states / 3 distinct spec

“There is at least one server that’s always online” could mean one of two things:

1. At any given point in time, there is at least one server online.

2. In every behavior, there is a particular server, and that server is online at all points in time.

(1) is a standard invariant. (2) is a safety property, but not an invariant. There is no individual state, by itself, that would violate it. Say I give you the state online = {1}. Is that a violation? Only if, in the behavior, there’s another state where 1 \notin online. So we can’t just look at a single state to know if we’ve broken (2) or not.

TLC can check (2) as a temporal property, though.

[] (always/”box”)

[]P means that P is true in every state. When on the outside of a predicate, this is equivalent to an invariant, and in fact is how TLC supports them: making P an invariant is the same thing as making []P a property.

Warning

Making P a property (without the box) will just check that P is true in the first state.

Things get more interesting when [] is part of a larger expression. Writing []P \/ []Q means every behavior has either P or Q as an invariant, but doesn’t need to have both. Or we could write []P => []Q, to say that P is a stronger invariant than Q. We can also put a [] inside a quantifier. To properly model (2), we could write:

Safety == \E s \in Servers: [](s \in online)

At the beginning of the behavior, we pick one online server. That server is then always online. This isn’t true: if we check with PROPERTY Safety, then we get an error trace.

 (*--algorithm threads
 variables 
   online = Servers;
+
+define
+  Invariant == \E s \in Servers: s \in online
+  Safety == \E s \in Servers: [](s \in online)
+end define;
 
 process orchestrator = "orchestrator"
 begin

(fails) spec

State 1: online = {"s1", "s2"}

State 2: online = {"s2"}

State 3: online = {"s1", "s2"}

State 4: online = {"s1"}

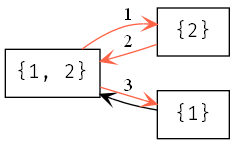
The behavior sequence 1-2-3 breaks violates our safety property, even though no state is individually a “bad state”.

In summary, adding [] to the language lets us represent all invariants, and a host of other properties too.

Anything can crash

[] is just a logical operator, like any other, meaning we can combine it with other logical operators. []~P means that P is always not true. ~[]P means that P isn’t always true. There are two things that could mean:

1. In every behavior, there is at least one state where P is false

2. There is at least one behavior which has at least one state where P is false.

Version (1) is more often useful in specs, so that’s what ~[]P formally means.1 If we write

 define
   Invariant == \E s \in Servers: s \in online
   Safety == \E s \in Servers: [](s \in online)
+  \* It's not the case that all servers are always online
+  Liveness == ~[](online = Servers)
 end define;
 
 process orchestrator = "orchestrator"

(fails) spec

This is a liveness property, not a safety property. In order to satisfy Liveness, the behavior has to reach a state where the server is offline.

We’d expect that to pass. The orchestrator can do one of two things: remove an existing server from online or add one that’s not in it. So if all the servers start online, then eventually we’ll remove one, right?

Not so fast! There’s a third thing the orchestrator can do: it can crash. In TLA+, any behavior is allowed to stutter, or make a new state where nothing happens and all variables are unchanged. This includes stutter-steps, meaning any behavior can stutter infinitely, aka crash. And that’s exactly what we see if we run the spec with PROPERTY <- Liveness:

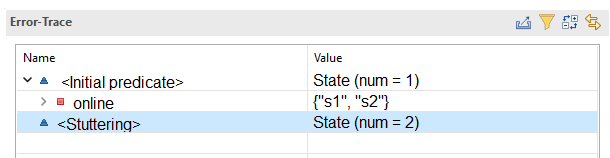
Note

Why haven’t we see this before? Because up until now we’ve only had invariants, which are only violated by “bad states”: particular configurations of variables that break the invariants. Stutter steps don’t change the values of anything, so a stutter step can never break an invariant. Here’s the first time it can break things by preventing us from reaching a good state.

TLA+ allows infinite stutter steps because it is fundamentally a worst-case scenario language. IN reality, systems always crash. If we do not explicitly say a system can’t crash, TLA+ will assume the system can crash at the worst possible time.

We can always keep stuttering at the {1, 2} state. Even though it could transition to either good state, it doesn’t have to.

So we need a way to say “don’t assume this system can crash”. We do this by saying it’s a fair process.

   Liveness == ~[](online = Servers)
 end define;
 
-process orchestrator = "orchestrator"
+fair process orchestrator = "orchestrator"
 begin
   Change:
     while TRUE do

5 states / 3 distinct spec

This makes the process weakly fair: it cannot “stop forever”. Once we add this change, we see Liveness holds. There’s also strong fairness. But this easier to explain (and more useful) in pure TLA+, as opposed to PlusCal. I’ll leave the PlusCal material in an advanced topic here.

Strong Fairness

Weak fairness says that if a process can always make progress, it will eventually make progress. Strong fairness is that if a process can always intermittently make progress, it will eventually make progress. To see the difference, consider this model of several threads sharing a lock (<> is defined below):

---- MODULE threads ----
EXTENDS Integers
CONSTANT NULL

Threads == 1..2

(*--algorithm threads
variable lock = NULL;

define
  Liveness == 
    \A t \in Threads:
      <>(lock = t)
end define;

fair process thread \in Threads
begin
  GetLock:
    await lock = NULL;
    lock := self;
  ReleaseLock:
    lock := NULL;
  Reset:
    goto GetLock;
end process;
end algorithm; *)
====

(fails) spec

When in GetLock, each thread can only get the lock if lock = NULL. So it’s only intermittently able to progress. Since every thread with the lock is guaranteed to release it, it’s always intermittently able to progress. In weak fairness, if we have five threads, we can’t guarantee that all five threads will eventually get the lock; one could get starved out.

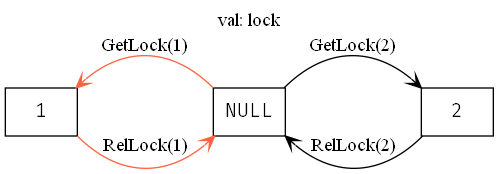
If thread 1 keeps stealing the lock, then thread 2 never has a chance to get it, even if it’s weakly fair.

We can make the processes strongly fair by writing fair+. Then every thread will eventually get the lock. We can also make individual actions strongly fair by writing AwaitLock:+.

       <>(lock = t)
 end define;
 
-fair process thread \in Threads
+fair+ process thread \in Threads
 begin
   GetLock:
     await lock = NULL;

15 states / 8 distinct spec

We’ll double back to strong fairness when we talk about writing Pure TLA+ specs, where we can do a little more with it.

Tip

Not every process in a spec needs to be fair. Consider a spec where one process represents the worker and one represents a user. The user actions aren’t guaranteed to happen: the user can always log off.

<> (eventually / “diamond”)

While ~[]P has some interesting properties, we rarely write it. It’s not often we need to check that something “is sometimes” not true in our system. What is useful is writing ~[]~P: “Sometimes ‘not P’ is false”, or “Sometimes P is true”. This means that P isn’t an invariant in all states, but must hold in at least one state.

Because “Not always not P” is a mouthful, we have a separate operator that means the same thing: <>P, or “Eventually P”. We’ve already been crudely simulating “eventually” properties before, in duplicates and threads. Here’s the correctness condition for threads:

AllDone ==
  \A t \in Threads: pc[t] = "Done"

Correct ==
    AllDone => counter = NumThreads

The AllDone => is just a precondition that counter = NumThreads is true at the end of the algorithm execution. Using <> we can rewrite it as a temporal property:

   lock = NULL;
 
 define
-  AllDone == 
-    \A t \in Threads: pc[t] = "Done"
-
-  Correct ==
-      AllDone => counter = NumThreads
+  Liveness ==
+    <>(counter = NumThreads)
 end define;  
 
 process thread \in Threads

(fails) spec

(Remember this is checked under “Temporal Properties”, not “Invariants”!)

When we run this with PROP Liveness, NULL <- [mv] the spec fails due to stuttering. There’s no guarantee the threads will finish running, because they’re unfair. This wasn’t a problem with Correct before because that only says that if we reach the end, then the answer is correct. It still passes if we never reach the end!

Making the threads fair makes this pass:

     <>(counter = NumThreads)
 end define;  
 
-process thread \in Threads
+fair process thread \in Threads
 variables tmp = 0;
 begin
   GetLock:

19 states / 17 distinct spec

In one way, Liveness is more accurate than Correct. In another way, though, it’s less accurate. Here’s a bug that wouldn’t pass Correct:

 (* --algorithm threads
 
 variables 
-  counter = 0;
+  counter = 1;
   lock = NULL;
 
 define

spec

When we’re done, counter = 3… but Liveness still passes! This is because <>(counter = 2) is true if counter = 2 in at least one state of the behavior. It doesn’t matter if we then change away from that, because it’s been true at least once.

Since it passes through a state where counter = 2, this passes <>counter = 2.

<>[]

Fortunately, our temporal operators are extremely flexible, and we can compose them together. If []P means “P is always true”, and <>P is “P is eventually true”, then <>[]P is “eventually P is always true”. P can start out false, but after some point in every behavior, it will forevermore be true.

 
 define
   Liveness ==
-    <>(counter = NumThreads)
+    <>[](counter = NumThreads)
 end define;  
 
 fair process thread \in Threads

(fails) spec

This now fails, as counter doesn’t stay as 2.

Since counter doesn’t converge on 2, this fails <>[]counter = 2.

Tip

You can also write []<>P: “P is always eventually true”. In the threads spec, this has the same outcome, but there are cases where it’s broader than <>[]P. For example, in an hour clock, []<>(time = midnight) is true, but <>[](time = midnight) is false.

~> (leads-to)

The last operator is ~>. Recall that P => Q preconditions Q on P: if P is true, then Q is also true. P ~> Q is the temporal analog: if P is true, then Q is eventually true (now or in a future state).

Say we have a set of tasks described by TaskType, an inbound pool of type SUBSET TaskType, and a set of workers with their own task sets. A property of this system might be that every inbound task is eventually processed by a worker. You can represent this with ~>:

Liveness ==
  \A t \in TaskType:
    t \in inbound
      ~> \E w \in Workers:
        t \in worker_pool[w]

Note

P ~> Q is triggered every time P is true. Even if the formula was satisfied before, if P becomes true again, then Q has to become true again too.

When to use Liveness

You probably won’t need to ever write a property of form \E x: [](P(x)).

Liveness properties are less common than invariants. Invariants check faster and give you finer-grained information, and they’re a lot easier to write! Most systems will have lots of invariants but only a couple of liveness properties. However, the liveness properties are still critical to the spec, as they define what it is we actually want to do.

Considerations

• It takes TLC significantly longer to test liveness properties than safety ones. Usually you’ll have one model that with large constants for testing safety properties, and a model with smaller constants for testing liveness properties.

• You cannot use symmetry sets with liveness properties.

• For implementation reasons, TLC can’t currently tell you which property is broken. It can only tell you “Temporal Properties are Violated”.

• Again, due to implementation details, error violations for liveness properties won’t be as-short-as-possible. You might get a shorter (and more understandable) error trace if you rerun the model with smaller constants.

Summary

• In addition to checking properties of states, TLA+ can check properties of entire behaviors.

• Safety properties are “bad things don’t happen”, liveness properties are “good things do happen”. All invariants are safety properties, and all liveness properties are temporal properties.

• All TLA+ specs are “stutter-invariant”, meaning they can crash at any time. A “weakly fair” process is guaranteed to “not crash”, though it can spinlock.

• []P means that P is true for every state of every behavior. <>P means that P is true for at least one state of every behavior. P ~> Q means that if P is true in a state, then Q will be true in a (present or) future state.

1

This isn’t “settled fact”: there are other systems where ~[]P only needs P to be false in one state of one behavior. These systems tend to be worse at modeling some things and better at modeling others.